1.3 Comparaison de plus de deux fréquences (test d'homogénéité)

Problématique

On étudie un caractère donné noté A à k modalités ou événements (comme les niveaux de gravité d'une maladie, des doses d'exposition à un polluant…) notées A1, … Ai, …Ak, dans un nombre l d'échantillons d'individus notés E1, .. Ej,…El.
On observe :
Oij, le nombre d'individus présentant la modalité Ai dans l'échantillon Ej:


La question est de savoir si les fréquences des modalités Ai entre chaque échantillon sont statistiquements égales (c'est l'hypothèse nulle H0 pour un test bilatéral) ou sont statistiquement différentes (c'est l'hypothèse alternative H1).
Ainsi on teste si les échantillons proviennent d'une même population (H0), ou de populations différentes (H1).

C'est ce que l'on appelle un test d'homogénéité.

Pour cela on calule d'abord le nombre théorique d'individus présentant la modalité Ai dans l'échantillon Ej, sous l'hypothèse H0,  notée Cij et on le compare avec de nombre d'individus observés Oij.

Cij = Si Tj / N

avec:
N: nombre total d'individus étudiés;
Si: nombre d'individus présentant la modalité Ai sur les N individus;
Tj: nombre d'individus dans l'échantillon Ej .

---

Tests à réaliser

1. Si tous les effectifs théoriques Cij sont plus grands que 5, alors on calcule effectue un test du Chi-2 à à (k-1)*(l-1) degrés de liberté.
   La statistique du test s'écrit:
   
   
   
   
2. Si au moins un des effectifs théoriques Cij est inférieurs à 5
   alors on effectue un test exact de Fisher.

---

Application des tests avec les logiciels R ou Epi Info

1. Test du Chi-2

Exemple :

Une enquête sur la rhinite allergique est réalisée dans 3 villes notées A, B et C. Dans chacune d'elle un groupe de sujets tirés au sort  est interrogé.
Dans la ville A, 24 personnes sur 86 déclarent avoir eu une rhinite allergique dans l'année,
dans la ville B, 14 personnes sur 79 déclarent avoir eu une rhinite allergique;
dans la ville C, 8 personnes sur 80 déclarent avoir eu une rhinite allergique.

On veut savoir si la prévalence de la rhinite allergique est la même entre les 3 villes,

On compare donc la fréquence de la rhinite entre les 3 villes:
ville A : fA = 24 / 86 = 0,279 soit 27,9 % de rhinite allergique;
ville B: fB = 14 / 79 = 0,177 soit 17,7 % de rhinite allergique;
ville C: fC = 8 /  80 = 0,10 soit 10 % de rhinite allergique;.

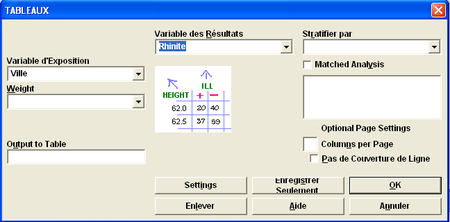
Dans le module Analyse des Données, on utilise la commande Tableaux pour réaliser un test du Chi-2, avec les variables Ville et Rhinite.

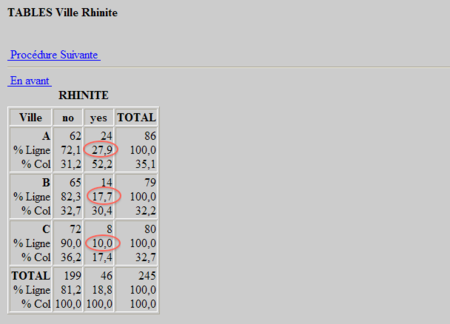
On obtient alors un tableau avec 3 lignes et 2 colonnes

Le résultat du test du Chi-2 est le suivant:

Si une des cases du tableau présentait un effectif attendu inférieur à 5, un message d'avertissement apparaitrait en dernière ligne du résultat. Comme ce n'est pas le cas ici, le test du Chi-2 est valable.
On regarde donc le résultat du test à la colonne "Probabilité" .

La probabilité (p-value) pour le test du Chi-2 est de 0,0123, soit inférieur au seuil de 0,05, on conclut donc que les prévalences de la rhinite allergique sont statistiquements différentes entre les 3 villes.



2. Test exact de Fisher

Exemple :

Une enquête sur la rhinite allergique est réalisée dans 3 villes notées A, B et C. Dans chacune d'elle un groupe de sujets tirés au sort  est interrogé.
Dans la ville A, 12 personnes sur 36 déclarent avoir eu une rhinite allergique dans l'année,
dans la ville B, 2 personnes sur 16 déclarent avoir eu une rhinite allergique;
dans la ville C, 1 personne sur 13 déclare avoir eu une rhinite allergique.

On veut savoir si la prévalence de la rhinite allergique est la même entre les 3 villes.

On compare donc la fréquence (la prévalence) de la rhinite entre les 3 villes:
ville A : fA = 12 / 36 = 0,333 soit 33,3 % de rhinite allergique;
ville B: fB = 2 / 16 = 0,125 soit 12,5 % de rhinite allergique;
ville C: fC = 1 /  13 = 0,08 soit 8 % de rhinite allergique;.


Le nombre attendu de personnes avec une rhinite allergique dans la ville C sous l'hypothèse nulle (les prévalences de rhinite dans les 3 villes sont les mêmes) est de:
15X13 / 65 = 3

(15: nombre de personnes avec la rhinite en tout;
13: nombre de personnes interrogées dans la ville C;
65: nombre total de personnes interrogées)

Comme ce nombre est inférieur à 5, on ne peut pas appliquer le test du Chi-2. On applique donc le test Excat de Fisher avec le logiciel R, car il n'est pas disponible sur Epi Info pour des tableaux de plus de 2 lignes ou 2 colonnes.

Voilà comment procéder avec R:

on crée d'abord un tableau de 3 lignes et 2 colonnes avec les données, que l'on met dans un objet appelé "tabrhinite".

 

Puis on applique le test de Fisher à ce tableau avec la fonction test.fisher()

Le p (p-value) obtenue est de 0,126 soit supérieur au seuil de signification de 0,05. On conclut donc qu'avec nos données, on trouve que les prévalences de la rhinite allergique ne sont pas statistiquement différentes.

Remarque: ce résultat peut être dû au manque de puissance de notre étude, car nous n'avons interrogé que 65 personnes en tout, dont 13 seulement dans la ville C.

---

Fiche récapitulative

Remarques:

Le test du Chi-2 est, au degrés de liberté près, le même que celui qu'on applique pour comparer 2 fréquences observées;

Epi Info ne calcule pas le test de Fisher pour des tableaux de données de plus de 2 lignes ou 2 colonnes, d'où l'utilisation du logiciel R à la place.