1.2 Comparaison de deux fréquences observées

Problématique

On étudie un caractère donné noté A (être malade, être exposé à un facteur de risque de maladie, avoir un symptôme…) dans deux populations d'individus notées G1 et G2.
On observe :
f1, la fréquence de la présence de A dans un échantillon d'individus de taille n1 tiré de la population G1;
f2, la fréquence de la présence de A dans un échantillon d'individus de taille n2 tiré de la population G2.

La question est de savoir si les fréquences de A de chaque population G1 et G2, notées p1 et p2 sont égales (c'est l'hypothèse nulle H0 pour un test bilatéral) ou sont statistiquement différentes (c'est l'hypothèse alternative H1), en comparant les fréquences observées f1 et f2.
C'est ce que l'on appelle un test d'homogénéité.

---

Tests à réaliser

1. Si la taille des échantillons est plus grand que 30 individus (n1 et n2 ≥ 30) et si le nombre d'individus avec le caractère A dans chaque échantillon est de plus de 5 (n1f1 et n2f2 ≥ 5), ainsi que le nombre d'individus ne présentant pas le caractère A  ( n1(1-f1) et  n2(1-f2) ≥5 ),
   alors on peut calculer la statistique U (correspondant à la différence entre les fréquences observées) qui, sous l'hypothèse nulle, suit une loi normale centrée réduite N (0,1).
   
   
   
2. Si, quelle que soit  la taille des échantillons n1 et n2, le nombre d'individus avec le caractère A dans un des échantillons est de moins de 5 (n1f1 ou n2f2 < 5), ou si le nombre d'individus ne présentant pas le caractère A  dans un des échantillons est de moins de 5 ( n1(1-f1) ou n2(1-f2) < 5 ),
   alors on effectue un test exact de Fisher.
   
   
3. Si la taille de l'un des échantillons est de moins  de 30 individus (n1 ou n2 < 30) et
   si le nombre d'individus avec le caractère A dans chaque échantillon est de plus de 5 (n1f1 et n2f2 ≥ 5), ainsi que le nombre d'individus ne présentant pas le caractère A ( n1(1-f1) et  n2(1-f2) ≥5 ),
   alors on effectue un test du Chi-2 à 1 degré de liberté.
   
   

---

Application des tests avec les logiciels  R ou Epi Info

1: Calcul de la statistique U

Exemple:
Pour tester l'efficacité d'un vaccin antigrippal, avant la saison de la grippe, on sélectionne un échantillon noté 1 de 100 personnes qui ne seront pas vaccinées, et un échantillon noté 2, de 200 personnes que l'on vaccine. A la fin de la saison on observe d'une part que 32 personnes non vaccinées ont eu la grippe, et d'autre part que 50 personnes issues de l'échantillon vacciné a eu également la grippe. On a donc la fréquence de la grippe dans chaque échantillon:
f1 = 32 / 100 = 0,32 dans l'échantillon des personnes non vaccinées;
f2 = 50 / 200 = 0,25 dans l'échantillon des personnes vaccinées.
Le vaccin est-il efficace ?

Pour le tester, on calcule la statistique U, car la taille de chaque échantillon est de plus de 30, et le nombre de personnes grippées est supérieur à 5.

Voilà comment on procède avec R en utilisant la fonction pnorm(x) qui donne la valeur de la fonction de distribution de la loi normale centrée réduite:
on calcule d'abord la statistique U, puis le probabilité critique pobs que la valeur u observée ait la valeur obtenue si l'hypothèse nulle est vraie.

On obtient pobs = 0,20 soit une valeur supérieure à 0,05, valeur seuil souvent retenue.
Donc on ne rejette pas l’hypothèse nulle, et on en conclut que la fréquence de la grippe est comparable entre le groupe des vaccinés et des non vaccinés, donc que le vaccin n'est pas efficace.

2. Test exact de Fisher

Exemple (tiré du projet exemple fourni avec Epi Info, sample.mdb, questionnaire ViewOswego):

A la suite d'un repas, des personnes ont une indigestion.
Parmi les 37 convives, 28 ont pris de la glace à la vanille en dessert, 9 n'en ont pas pris.
On veux tester si l'indigestion peut être dûe à la prise de cette glace.
On compare donc la fréquence de l'indigestion chez les 28 personnes qui ont pris de la glace (22 sur 28), et celle chez les 9 convives qui n'ont pas pris de glace (1 sur 9).
On a donc :
f1 = 22 / 28 = 0,786 soit 78,6 % de malades chez les personnes ayant pris de glace;
f2 = 1 / 9 = 0,111 soit 11,1 % de malades chez les personnes n'ayant pas pris de glace.

Le nombre de personnes malades n'ayant pas pris de glace étant de 1 (donc inférieur à 5) on doit appliquer le test exact de Fisher.

Avec Epi Info, on peut utiliser le module Analyse des Données si on a le fichier de données, ou le module StatCalc.

Dans le module Analyse des Données, on utilise la commande Tableaux.
On obtient alors le tableau croisé entre la variable prise de glace à la vanille ("Vanilla Ice Cream") et la variable avoir une indigestion ("ill"):

Le résultat des tests est le suivant:

on ne regarde que le test exact de Fisher à la fin, comme l'indique l'avertissement d'Epi Info à la dernière ligne.

Dans le module StatCalc, on choisit le programme Tables (2 X 2, 2 x n), puis on rentre les données sous forme de tableau 2x2.

Le résultat est le suivant:

On ne regarde que le test exact de Fisher en bas, comme l'indique le message en anglais d'Epi Info à la dernière ligne.

Le p (p-value) étant inférieur à 0,0006, soit bien inférieur au seuil de 0,05, on conclut que les fréquences des personnes malades entre celles qui ont pris de la glace et celles qui n'en ont pas pris sont statistiquement différentes, donc que la glace à la vanille est vraisemblablement la cause de l'indigestion.

3. Test du Chi-2

Exemple (tiré du projet exemple fourni avec Epi Info, sample.mdb, questionnaire ViewOswego):

A la suite d'un repas réunissant 75 convives, 46 ont eu une indigestion.
23 personnes ont pris de la gelée en dessert, 52 n'en ont pas pris.
On veux tester si l'indigestion peutêtre dûe à cette prise de gelée.
On compare donc la fréquence de l'indigestion chez les 23 personnes qui ont pris de la gelée (16 sur 23), et celle chez les 52 convives qui n'ont pas pris de gelée (30 sur 52).
On a donc :
f1 = 16 / 23 = 0,696 soit 69,6 % de malades chez les personnes ayant pris de la gelée;
f2 = 30 / 52 = 0,577 soit 57,7 % de malades chez les personnes n'ayant pas pris de la gelée.

Le nombre de personnes ayant pris de la gelée étant inférieur à 30 (23), et dans chaque case du tableau l'effectif étant supérieur à 5, on doit appliquer le test du Chi2.

Avec Epi Info, on peut utiliser le module Analyse des Données si on a le fichier de données, ou le module StatCalc.

Dans le module Analyse des Données, on utilise la comande Tableaux.
On obtient alors le tableau croisé entre la variable prise de la gelée ("Jello") et la variable avoir une indigestion ("ill"):

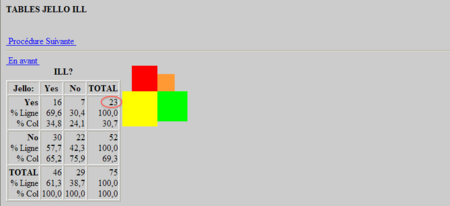
Le résultat des tests est le suivant:

On regarde le résultat du test à la ligne,"Chi-quarré - non corrigé", colonne "2-tailed p" .

Dans le module StatCalc, on choisit le programme Tables (2 X 2, 2 x n), puis on rentre les données sous forme de tableau 2x2.

Le résultat est le suivant:

On regarde le résultat du test à la ligne "Uncorrected", colonne "P-values" .


Le p (p-value) pour le test du Chi-2 est de 0,33, soit bien supérieur au seuil de 0,05.

On conclut donc que les fréquences des personnes malades entre celles qui ont pris de la gelée et celles qui n'en ont pas pris ne sont pas statistiquement différentes, et donc que la gelée ne semble pas être la cause de l'indigestion.

---

Fiche récapitulative

Remarque:

en pratique, si l'effectif des 2 groupes est supérieur à 30, et les effectifs attendus dans les 4 cases du tableau 2X2 des données sont supérieurs à 5, on réalise un test du Chi-2, plutôt que de calculer la statistique U.

Comments

[Christophe]

Pour le calcul de u, il faut la valeur absolue de f1-f2, sous R : abs(f1-f2)